連続系と計算機のちょっと近い関係

はじめに

非常に多くの物理現象は場の相互作用によってよく表されます。そして、その相互作用は絶対座標に依存しない局所的な時間発展を示す偏微分方程式で表されることになります。これらの経験的あるいは解析的な簡略化として、何らかの離散化が行われます。*1工学というのはこれらの簡略化の上に成り立っているわけです。

一方それとは全く異なる方向性として、知性によるもの、つまり概念のシンボル化と操作に基づく体系があります。近代の数学や計算機科学が挙げられますが、前者はともかく後者は物理的実体として実装される必要があって、それは前述の方法によって成されます。

さてここで気になるのは、(チューリング完全な)計算というのは本質的に複雑なプロセスであって*2、それは簡略化とは相容れないということです。つまり、モデル化により一度失われた複雑さをどこで取り戻すかというのが問題になります。

そして現在の状況はというと、できるだけ高速な信号伝送と論理演算を実現し、時間は同期信号で離散化してしまって有限状態機械を構築するということをしているわけです。つまり物理系の複雑性は命題論理に残るのみで、実際の空間と時間は捨象されてしまいます。

時間や空間のような重要な要素を捨ててしまわずに、計算を行う方法としてはセルオートマトン(CA)が挙げられます。これは座標の離散化は行うものの、時間発展に近くの状態しか使わないという点で、「広さ」が維持されていると言えるでしょう*3 *4

しかし、このように物理的な系により近いはずのCAですが、実際にそれを再現するような連続な系を構成した例は見当たらないようです。

そこで、今回はその中でも特に簡単な、一次元の基本セルオートマトン(ECA)*5を再現することにしました。ECAは単純なものの、ルール110と呼ばれている遷移規則を用いるとチューリング完全になることが証明されています*6。

以下ではその具体的な方法について述べます。

定義

この節ではECA、連続系、二者の間の対応づけの定義を行い、構成の合理的な制約及び指針として用いる。

ECA

整数とその近傍によって定められる無限グラフ上で、各点はその位置 $x\in Z$ と時刻 $t\in Z$ により定まる状態 $\{0,1\}$ を持ち(これを $q(x,t)$ とする)、以下の遷移関数 $\phi$ を持つ。

$\forall x,t. q(x,t+1)=\phi(q(x-1,t),q(x,t),q(x+1,t))$

なお、この $\phi$ には $2^{2^3}=256$ 通りしか無く、ある規則*7 *8に従ってルール0からルール255と呼ばれる。

連続系

空間は再現するECAに合わせて一次元
時間と空間の並進移動に対して不変(つまり $t,x$ が単体で表われない)
実数値をとる複数のスカラー場
時間微分は一階まで、空間微分は何階でも良い *9

つまり、 $u_1(x,t)\ldots u_n(x,t)$ について、
初期条件 $u_i(x,0)=c_i(x)$ と
時間発展 $\frac{\partial u_i}{\partial t}=F_i(\{\frac{\partial^\beta u_\alpha}{\partial x^\beta}\}_{\alpha,\beta}) (\beta \ge 0)$
とする。

また、 $u_j=F_j(\{u_\alpha\}) (F_j\in C^\infty)$ 場は機械的に上記の形式に変換でき、便宜上このような形式を考えることは有用である。

対応

連続体における離散的な構造の創発は大変興味深い現象ではあるが、ここでは後述する定在波格子を用いることとし、対応付けを以下のように定義する。

ECAのルール $r$ から支配方程式への写像が存在する $\mathcal{G}r=\{F_i\}$
ECAの状態 $s:\{0,1\}^Z$ から、ある一瞬における全ての場が定まる(便宜上これを初期状態とする) $\mathcal{S}s=\{c_i\}$
$r,s$ によらない定数 $\theta,\lambda,T$ が存在し、1,2によって定まる系の発展によりECAの状態 $q$ は次のように表される $q(x,t)=b(u_1(\lambda x,Tt)) (t\ge 0)$

(但し $b(x)=1 (x>\theta)$ , $b(x)=0 (otherwise)$ とする)

これらの $(\mathcal{G},\mathcal{S},\thet,\lambda,T)$ を定められることを、ECAを連続系でエミュレート可能であるとする。

構成方法

まず構成法を概観し、そののち各部分の構成とそれらが相互に干渉しないことを述べる。

概要

(図1: 情報の流れと格子構造)

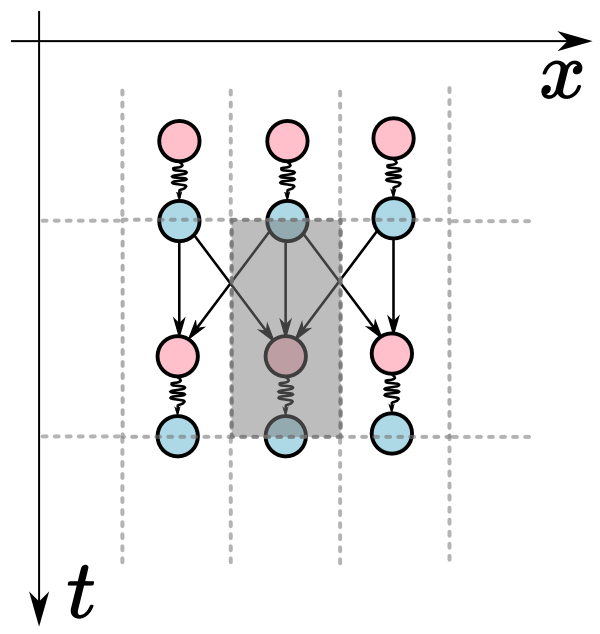
丸で示す、周期が同じで位相のずれた2つの格子があり、それにより値の局在化を行う。
赤丸では近傍から集められた状態にルールを適用し、次の状態を確定させる。そこから波線で値は青丸に伝えられ、青丸では値の増幅を行うことで近傍への状態伝送に備える。状態の伝送は移動性のある別の場を介することで行われる。

灰色の領域を単位格子とし、これらの相互作用が連続体内で周期的に発生することでエミュレーションを行う。

定在波格子

(図2: 二重の格子)

定数 $k,\omega$ について、 $c_\pm(x)=\sin(\pm kx)$ と $\frac{\partial u_\pm}{\partial t}=\pm \frac{\omega}{k}\frac{\partial u_\pm}{\partial x}$ による与えられる場はそれぞれ解析解 $u_\pm(x,t)=\sin(\omega t\pm kx)$ を持ち、
これらの和は定在波 $(u_+ +u_-)(x,t)=2\sin(\omega t)\cos(kx)$ となる。初期条件における同相の位相差は時間、逆相の位相差は位置におけるずれとして現れ、この2つのパラメータは独立に制御できる。また、例えば $(\frac{u_+ +u_-}{2})^{2m}\ge 0$ は図1の丸のように格子状に並んだピークを作ることができる。

今回は時間方向にずれた格子を図2のように二個用いる。機能と色の関係は図1と同じで、青を $u_{tx}$ 、赤を $u_{rx}$ と呼ぶことにする。

増幅

(図3: 飽和関数 $\sigma(x)=-1+2/(1+\exp(-ax^n)) (n=1,3)$ )

シグモイド関数の変形により、図3のように2値または3値に飽和させる関数を定義できる。常微分方程式 $f'(t)=\frac{c-f(t)}{\tau}$ は値 $c$ に向かって時定数 $\tau$ で漸近してゆく変化を表すが、 $f'(t)=\frac{\sigma(f(t))-f(t)}{\tau}$ とすることで、値をすみやかに離散化することができる。この負帰還が働いている状態ではある値より小さい変化は無視されるので、例えば空間的な拡散と組み合わせることが可能になる。

局在化

格子を用いて、時空の領域ごとに作用を切り替えることができる。例としては、 $\frac{\partial u}{\partial t}=u_{tx}F_{tx}+u_{rx}F_{rx}+(1-u_{tx}-u_{rx})F_{out}$ にような加重和が挙げられる。特に $F_{out}$ を急速な減衰に設定することで、値が別のピークに移動しないように制御できる。

また、ひとつのピークに対応する領域内において、空間的な振動が発生し複数の値を持ってしまうと離散化が損なわれる。そこで空間の二回微分(拡散項)を加えることで混合し、ある一つの値がドミナントになるように調整を行う。

伝送

(図4: 値の伝送)
伝送には、値の保持とは別の場を、各方向ごとに用意する。受け入れ格子( $u_{rx}$ )では0に、送り出し格子( $u_{tx}$ )では保持された値に漸近することで、情報伝送の始点と終点を定める。その間では飽和と拡散を合わせることで、ほぼ一定幅で値を保持し、また空間の一階微分の項により移動が可能である(図4の左と右)。

論理演算

飽和関数 $\sigma$ を用いてブール代数を実装することは容易である。例えば、2入力論理和(2-OR)は $\sigma(a+b+1)$ 、3入力論理積(3-AND)は $\sigma(a+b+c-2)$ のように記述できる。遷移関数 $\phi$ は左近傍 $q__$ 、右近傍 $q_+$ 、自分自身の値 $q_0$ からなる8通りの項 $\bar{q_-}\bar{q_0}\bar{q_+},\ldots,q_-q_0q_+$ の組み合わせからなる積和標準形と同値であり、ルール番号の各ビットはこの項を加えるかどうかを表している。

これにより次の状態で取る値 $u_{app}$ を $u_{app}=F(u_{trans,left},u_{trans,forward},u_{trans,right})$ のように計算できる。

情報フロー

(図5: 位置固定での時間変化)

図5は以上を踏まえて、ある位置での各場の時間変化を模式的に示したものである。先程示した手法の組み合わせで、…|app→val(rx)→val(tx)→trans|app→…と伝わっていることが分かる。

結果

ルール90( $u_{trans,l},u_{trans,f},u_{trans,r}$ )

ルール110( $u_{val}$ )

ルール110( $u_{tx},u_{rx},u_{app}$ )

まとめのようなもの

これまでで、最初に述べたエミュレーションの定義を満たしていることが、なんとなく分かるかと思います。これでめでたく、連続系もちゃんと計算できるということが示されたわけです。が、いくつか(いくつも)未解決の課題もあります。そのうちいくつかを示して終わりにしましょう。

(数学的に厳密な)解の存在と一意性の証明

常微分方程式に関しては、Picard-Lindelöfの定理という便利な物がありますが、PDEではどうでしょう？この系では値も有界、微分も有界なので、 $L^\infty$ 空間に関して積分を拡張してやれば証明できるかもしれないとも思いましたが、私には荷が重かったようです。

(工学的にもっともらしい)安定性の証明

果たしてどんな初期条件でも本当に安定するのか、何らかのモデルを作れるかもしれませんが、今回の構成例は特に実際の物理系とは関係ないのであまり意味がないかもしれません。

時間の進行方向について

仮に、有界性や連続性が解の存在に充分な条件ならば、時間を逆行することが可能ということになりますが、数値積分でこれをやってみるとすぐに発散します。しかし本物の実数体なら、値のごくわずかなぶれに過去の状態が記録されている可能性もあります。また、エネルギー、エントロピーとの関係は？

格子の自己組織化

今回用いた格子は正弦波ですが、これは単純な解析解を持つものの、何の帰還もかかっていないため数値積分ではいずれ発散してしまいます。そこで、同じような構造を持った格子を安定的に生成できないかという(例えばvan der Pol振動子のように)問題があります。

トポロジーの動的変化

特にいわゆるtotalisticなルールでは近傍の数が途中で変わっても自然な定義が可能と思われますが、その場合計算はどうなるのかという問題があります。

追記(2011/7/18)

オンラインで動くデモを用意しました。(Chromeで動作確認)
http://www.xanxys.net/ECA/
Visualization Schemeのあたりを適当に選んでredrawしてみてください。

追記(2011/10/5)

逆超離散化による構成が2004年には既に存在していたようです。
http://jpsj.ipap.jp/link?JPSJ/73/2033/

*1:線形化はとりうる状態のパターン(つまり基底)の離散化と捉えられるでしょう

*2:digital physicsの立場を取るならばそれより高度な計算は不可能

*3:一見すると時刻は無限に速い信号による同期が必要ですが、これは機械的に非同期なモデルに変換することができます

*4: L. Nehaniv, Self-Reproduction in Asynchronous Cellular Automata, http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.7.2073

*5: http://en.wikipedia.org/wiki/Elementary_cellular_automaton

*6:M. Cook, Universality in Elementary Cellular Automata, http://www.complex-systems.com/Archive/hierarchy/abstract.cgi?vol=15&iss=1&art=01

*7:wikipediaのECAの項目 http://en.wikipedia.org/w/index.php?title=Elementary_cellular_automaton&oldid=433936069

*8:S. Wolfram, Statistical mechanics of cellular automata, http://www.ifsc.usp.br/~lattice/artigo-wolfram-cellular-autom.pdf

*9:これには数値積分が簡単に書けるというメリットがあります