三次元回転の確率分布
唐突ですが、三次元空間内での回転の確率分布というのを考えてみます。回転の距離、回転の表現、超球面上の分布、回転の分布、という順番に見ていきます。
回転の距離の定義
まず、単一の回転の角度
、というのを考えてみましょう。不変な場合は0になって欲しいので
となりますが、それ以外ではどうでしょう。
ちょっと考えてみると、じゃない回転は回転軸との正の角度に分解できるので、その角度のうち最小のものを使って、
としてやれば良さそうです。このとき
となります。
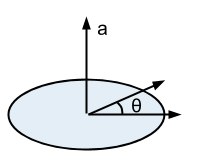
ちなみに、この角度aは、全ての三次元単位ベクトルについて
と
の角度の最大値をとったものに等しいです。
このを使うと、二つの回転の距離
は
と書けます。で、これが以下の距離の公理を満たしているか順番に見てみます。
- 非負性:
- 対称性:
- 三角不等式:
- 非退化性:
まず、fの値域から非負性は満たされます。
なので対称性もあります。
三角不等式はちょっとややこしいですが、は
から
まで最短で回転させる角度にもなっている(ような気がする)ので、その経路上に
が乗ってれば
になって、それ以外では遠回りになると考えると成り立ちそうです。
で、最後の非退化性ですが、はすぐにわかって、
なら
で、
なので問題なく成り立ちます。これで
が距離であると言えるでしょう。
単位クオータニオン
さて、みなさんご存知の通り(?)、三次元の回転は単位クオータニオンで表すこともできます。クオータニオンはスカラーと三次元ベクトルの組み合わせとして書くことができます。*1そのうちノルムが1のものを単位クオータニオンと呼んで、うまいことベクトルの回転の規則を選んでやると、角度が
と
を満たし、軸が
な回転を表します。
回転の合成はクオータニオンの積で表せます。他にも、共役
は
の逆の回転になります。
3自由度を表すのに4つの実数しか使ってなくて、オイラー角みたいな汚い問題(ジンバルロックとか)も発生しないのでよく用いられているらしいです。この素晴らしい表現を維持したまま、確率分布を考えたいわけです。
von Mises-Fisher分布
任意の次元の超球面上の分布のひとつにvon Mises-Fisher分布というのがあるらしく、pdfは次のようになります。
但し
よくみるとexpの中にはが入っていて、これで
との距離を計っているのが分かります。
回転の確率分布
さて、クオータニオンの要素の順番には意味があるので、これをさっきのvMF分布に直接突っ込んでしまっても果たして意味のある分布が得られるのかが問題になります。vMFではと
の内積を考えていたので、クオータニオンの内積が序盤で定義した回転の距離とどう関係するのか考えてみます。
回転を単位クオータニオン
で表すこととすると、
となります。そこで、
を計算してみると次のようになります。
この結果のスカラーの部分(相当)を見てみると、これは
を単純に四次元のベクトルとみなして内積をとったものに等しくなっています。というわけで、四次元空間でのクオータニオンふたつの角度の半分が、それらのクオータニオンが表す回転の角度になっていることがわかります。正直この辺のイメージはあまり鮮明ではないですが、一応めでたくvMF分布を使えそうです。